Heat Conduction in a Two-Dimensional Fin (Gmsh Example)

This page demonstrates solving the 2D heat conduction fin problem using a Gmsh-generated mesh. Gmsh is a powerful mesh generation tool that can create complex geometries and meshes for finite element analysis. For the mathematical formulation and theory, see the main (standard) tutorial.

Gmsh File Import

This example demonstrates how to import a Gmsh-generated mesh (.msh file format) and solve a heat conduction problem. 

<script type="module">
  import { FEAScriptModel, importGmshQuadTri, plotSolution, printVersion } from "https://core.feascript.com/src/index.js";

  window.addEventListener("DOMContentLoaded", async () => {
    // Print FEAScript version in the console
    printVersion();

    // Fetch the mesh file
    const response = await fetch("./rect_quad_unstruct.msh"); // .msh version 4.1 is currently supported
    if (!response.ok) {
      throw new Error(`Failed to load mesh file: ${response.status} ${response.statusText}`);
    }
    const meshContent = await response.text();

    // Create a File object with the actual content
    const meshFile = new File([meshContent], "rect_quad_unstruct.msh");

    // Create a new FEAScript model
    const model = new FEAScriptModel();

    // Set solver configuration
    model.setSolverConfig("solidHeatTransferScript");

    // Parse the mesh file first
    const result = await importGmshQuadTri(meshFile);

    // Define mesh configuration with the parsed result
    model.setMeshConfig({
      parsedMesh: result,
      meshDimension: "2D",
      elementOrder: "quadratic",
    });

    // Define boundary conditions using Gmsh physical group tags
    model.addBoundaryCondition("0", ["constantTemp", 200]); // bottom boundary
    model.addBoundaryCondition("1", ["constantTemp", 200]); // right boundary
    model.addBoundaryCondition("2", ["convection", 1, 20]); // top boundary
    model.addBoundaryCondition("3", ["symmetry"]); // left boundary

    // Set solver method
    model.setSolverMethod("lusolve");

    // Solve the problem and get the solution
    const { solutionVector, nodesCoordinates } = model.solve();

    // Plot the solution as a 2D contour plot
    plotSolution(
      solutionVector,
      nodesCoordinates,
      model.solverConfig,
      model.meshConfig.meshDimension,
      "contour",
      "solutionPlot",
      "unstructured" // Important: specify unstructured mesh type
    );
  });
</script>

Important notes about the Gmsh workflow:

  1. Physical Groups in Gmsh: In your .geo file, you need to define physical groups for boundaries using commands like Physical Line("bottom") = {1};. These are mapped to tags in the imported mesh.
  2. Boundary Condition Mapping and Tag Indexing: When using Gmsh meshes in FEAScript, you need to subtract 1 from the Gmsh physical group tag numbers. For example, if your Gmsh file has physical groups with tags 1, 2, 3, and 4, you would reference them in FEAScript as "0", "1", "2", and "3" respectively: model.addBoundaryCondition("0", ["constantTemp", 200]); // Gmsh physical group tag 1. This conversion is necessary because Gmsh uses 1-based indexing while FEAScript uses 0-based indexing.
  3. Unstructured Plotting: When plotting results from a Gmsh mesh, add the "unstructured" parameter to the plotSolution function to ensure correct visualization.

You can create your own Gmsh files by writing .geo scripts or using Gmsh's GUI. For this example, we used a simple rectangular domain defined in a .geo file with specific physical groups for each boundary.

Example Gmsh .geo File

Below is the rect.geo file used in this tutorial. It defines a 4m × 2m rectangular domain with physical lines for each boundary edge: 

// 2D Rectangle: 4m (width) x 2m (height)
// With Physical Lines for boundary labeling
// Use the command "gmsh rect.geo -2" to generate the mesh

lc = 0.7; // Characteristic length (mesh density)

// Points (x, y, z, mesh size)
Point(1) = {0, 0, 0, lc};     // Bottom left
Point(2) = {4, 0, 0, lc};     // Bottom right
Point(3) = {4, 2, 0, lc};     // Top right
Point(4) = {0, 2, 0, lc};     // Top left

// Lines
Line(1) = {1, 2}; // bottom
Line(2) = {2, 3}; // right
Line(3) = {3, 4}; // top
Line(4) = {4, 1}; // left

// Line Loop and Surface
Line Loop(1) = {1, 2, 3, 4};
Plane Surface(1) = {1};

// Physical Lines
Physical Line("bottom") = {1};
Physical Line("right")  = {2};
Physical Line("top")    = {3};
Physical Line("left")   = {4};

// Physical Surface (optional, for FEM domains)
Physical Surface("domain") = {1};

// Generate 2D mesh
Recombine Surface{1}; // Turn triangle elements into quadrilaterals
Mesh.ElementOrder = 2; // Set quadratic elements 
Mesh 2;

Note how the physical line tags in the geo file correspond to the boundary conditions in our FEAScript code:

To generate a mesh file from this .geo script, you would run: gmsh rect.geo -2 in your terminal, which creates a rect.msh file that can be imported into FEAScript.

Generated Mesh

Below is a visualization of the quadrilateral mesh generated by Gmsh. Notice how Gmsh creates an unstructured mesh with irregular elements that could potentially adapt to complex domain features.

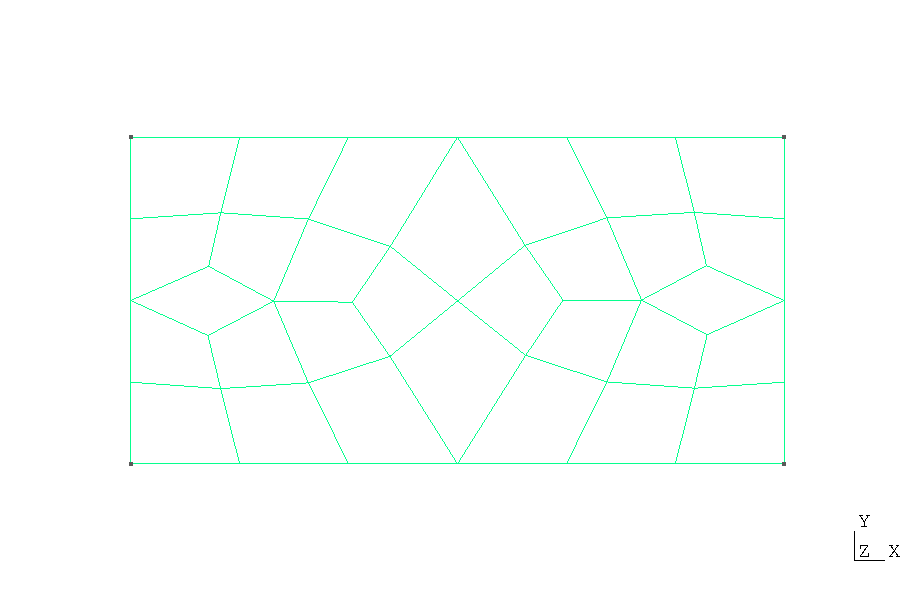
Quadrilateral mesh generated by Gmsh

Quadrilateral mesh (rect_quad_unstruct.msh) generated using the rect.geo script with Gmsh

The mesh consists of quadrilateral elements with varying sizes and shapes. This unstructured mesh approach would be particularly advantageous for complex geometries. FEAScript's Gmsh reader properly handles this unstructured mesh format and maps the elements and boundary conditions.

Results

Below is the 2D contour plot of the computed temperature distribution. This plot is generated in real time using FEAScript. Please note that solutions computed on unstructured meshes like this may exhibit small numerical differences compared to solutions on structured orthogonal meshes. This occurs because derivative calculations in non-orthogonal elements are inherently less precise due to the Jacobian transformation process. These small differences are expected and acceptable for most engineering applications, but may be noticeable in regions with steep temperature gradients.

© 2023- FEAScript