

In this tutorial, we address a stationary heat transfer problem within a 2D rectangular domain. This is a typical cooling fin problem. Cooling fins are commonly used to increase the area available for heat transfer between metal walls and poorly conducting fluids such as air.
Steady heat conduction is described by the Laplace equation: \(\nabla^{2}T(x,y) = 0\), where \(T\) signifies the temperature values.
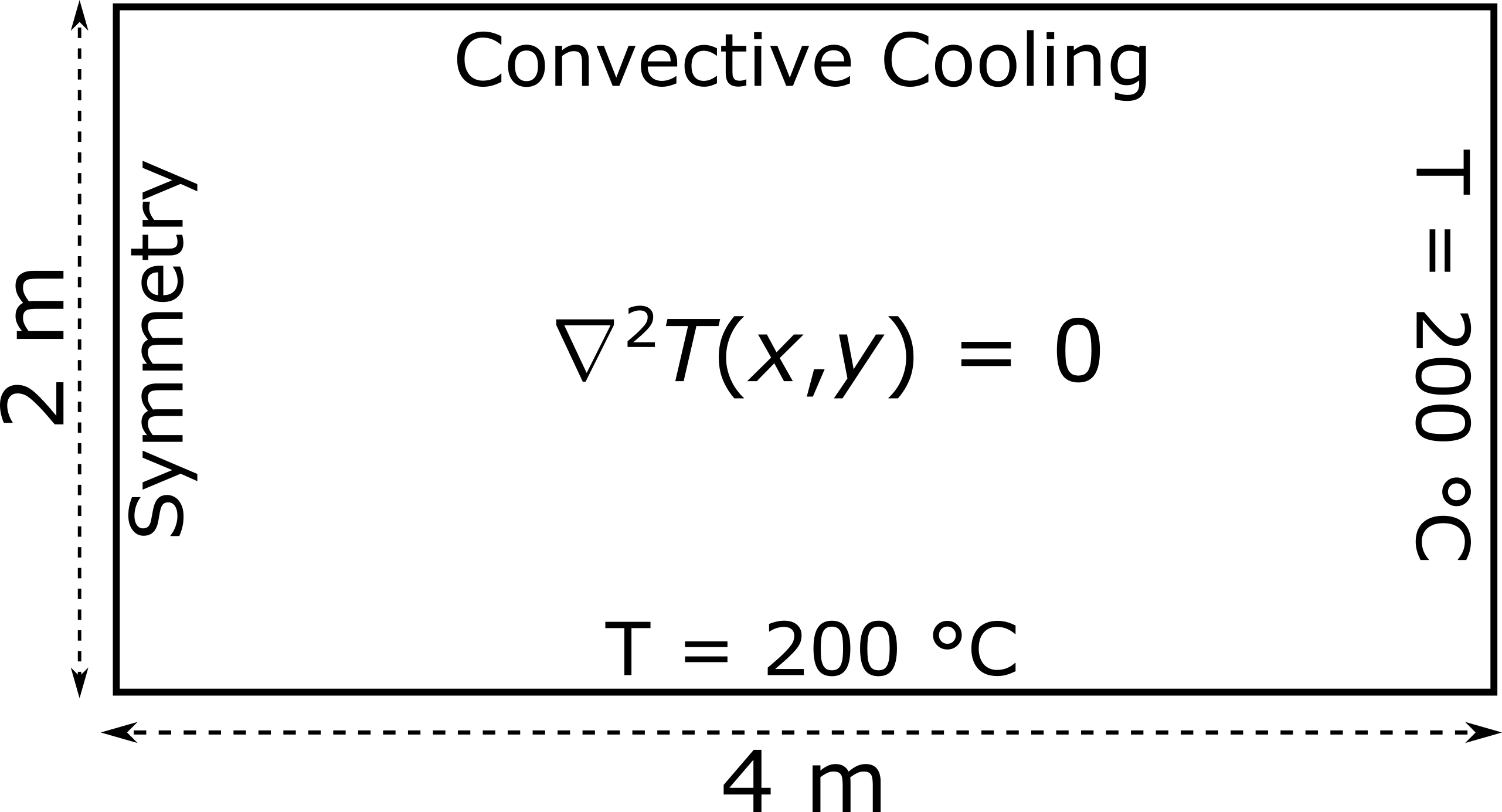
The above schematic illustrates the problem domain and outlines the associated boundary conditions. The constant temperature boundary conditions are implemented as Dirichlet types in the finite element code. The symmetry boundary condition is implemented as a Neumann zero-flux type \( \left( \frac{dT}{dx}|_{x=0}=0 \right) \), while the convective cooling boundary condition is of the Robin type. Specifically, the latter is expressed as \(\frac{dT}{dy}|_{y=4}=-{\frac{h}{k}}(T-T_0)\), where \(h\) is the heat transfer coefficient, \(k\) the thermal conductivity and \(T_0\) is the external temperature. We assume here that \({\frac{h}{k}}\) = 1 m-1 and \(T_0\) = 20 °C.
Below is a demonstration of how to use the FEAScript library to solve the stationary heat transfer problem in your web browser. You only need a simple HTML page to run this example where the following code snippets should be included. First, we should load the required external libraries: Math.js for the LU decomposition linear system solver, and Plotly.js for plotting the results. These libraries are loaded using the content delivery network (CDN) for portability. The code snippet is as follows:
<head>
. . .
<script src="https://cdnjs.cloudflare.com/ajax/libs/mathjs/5.0.0/math.min.js"></script>
<script src="https://cdnjs.cloudflare.com/ajax/libs/plotly.js/2.27.0/plotly.min.js"></script>
. . .
</head>
We should then define the problem parameters, such as the solver type, the geometry configuration, and the boundary conditions. This is performed using external JSON files.
The first JSON file, `solverConfig.json`, determines the solver type:
{
"solverConfig": "solidHeatTransferScript"
}
The second JSON file, `meshConfig.json`, concerns the computational mesh parameters. In particular, the parameters `numElementsX` and `numElementsY` represent the number of elements along the x-axis and y-axis, respectively. Additionally, `maxX` and `maxY` denote the final x-coordinate and y-coordinate of the mesh, respectively. When this file is fetched into FEAScript, a simple mapped mesh will be generated. The JSON file is structured as follows:
{
"meshDimension": "2D",
"elementOrder": "quadratic",
"numElementsX": 8,
"numElementsY": 4,
"maxX": 4,
"maxY": 2
}
The third essential JSON file, `boundaryConditionsConfig.json`, concerns the boundary conditions. Initially the numbers at the left side (from 0 to 3) indicate the boundaries of the geometry (the mesh generator of FEAScript has assigned numbers to the boundaries, starting from the bottom boundary and proceeding clockwise). The `constantTemp` condition sets a constant temperature value. The `symmetry` boundary condition represents a zero-flux type. Finally, the `convection` condition describes a convective heat transfer scenario. In addition, the second argument of the `constantTemp` boundary condition corresponds to the constant temperature value. For a `convection` boundary condition, the second argument represents the \({\frac{h}{k}}\) value, and the third argument indicates the external temperature \(T_0\). The JSON file is structured as follows:
{
"0": ["constantTemp", 200],
"1": ["symmetry"],
"2": ["convection", 1, 20],
"3": ["constantTemp", 200]
}
The above JSON files can be hosted online, for example, using GitHub Pages or other services dedicated to JSON file hosting, such as JSON Keeper. In our case, the JSON files are hosted on the FEAScript website. While it is also possible to load JSON files locally, hosting them online—or using a local Python server—can offer a safer and more reliable solution by adhering to Cross-Origin Resource Sharing (CORS) policies, which enhance security in web applications. These files are then fetched into FEAScript using the following script:
<body>
. . .
<script>
let meshConfig, boundaryConditionsConfig, solverConfig;
// Function to fetch and parse JSON files
function fetchJSON(url) {
return fetch(url).then((response) => response.json());
}
// Fetch all JSON files asynchronously
Promise.all([
// Solver configuration file
fetchJSON("https://feascript.com/tutorialSolidHeatTransfer01/solverConfig.json"),
// Computational mesh configuration file
fetchJSON("https://feascript.com/tutorialSolidHeatTransfer01/meshConfig.json"),
// Boundary conditions configuration file
fetchJSON("https://feascript.com/tutorialSolidHeatTransfer01/boundaryConditionsConfig.json"),
]).then(([solverConfigData, meshConfigData, boundaryConditionsConfigData]) => {
solverConfig = solverConfigData.solverConfig;
meshConfig = meshConfigData;
boundaryConditionsConfig = boundaryConditionsConfigData;
});
</script>
. . .
</body>
Finally, the `solidHeatTransferScript` solver is utilized which implements the finite element method for heat conduction problems. The solver accepts the above configuration JSON files (`solverConfig`, `meshConfig`, `boundaryConditionsConfig`) as inputs and returns the grid points (`nodesXCoordinates`, `nodesYCoordinates`) and the solution vector (`solutionVector`) as outputs. The following script demonstrates the solution process:
<body>
. . .
<script type="module">
// Import the FEAScript library
import { FEAScript, plotSolution, printVersion } from "https://feascript.github.io/FEAScript/src/index.js";
window.addEventListener("DOMContentLoaded", (event) => {
// Print FEAScript version
printVersion();
// Assemble matrices and solve the system of equations
let { solutionVector, nodesCoordinates } = FEAScript(solverConfig, meshConfig, boundaryConditionsConfig);
// Visualize the solution
plotSolution(solutionVector, nodesCoordinates, solverConfig, meshConfig.meshDimension, "contour", "solutionPlot");
});
</script>
. . .
</body>
After the solution, the results are demonstrated in a 2D contour plot. To do so, an HTML container element should also be included as follows:
<body>
. . .
<div id="solutionPlot"></div>
. . .
</body>
The `solutionPlot` is the id of the div where the plot will be rendered. This id is passed as an argument to the plotSolution function to specify the target div for the plot.
The results visualized in the following contour plot are generated real-time in your browser, according to the JSON files provided. The source code of the above tutorial can be found at the corresponding example directory.